Implicit relations arise when an equation combines x and y without solving explicitly for one variable, so identifying critical points requires careful reasoning about the derivative’s behavior along the curve.

Understanding Critical Points on Implicit Relations

A critical point is a location on a curve where its instantaneous rate of change meets specific conditions. For implicit relations, these points occur where the derivative with respect to x is either zero or undefined. Because the curve is not written as y = f(x), we rely on implicit differentiation to uncover the behavior of the relation and determine where these special points occur.

A valid critical point must satisfy two conditions: it must lie on the curve itself, and the slope information from the derivative must reveal either a horizontal or vertical tangent. These conditions ensure that the point genuinely reflects meaningful behavior in the geometric structure of the relation.

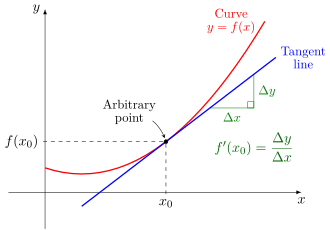
This graph shows a smooth curve with a tangent line touching it at one point, illustrating how the slope of the tangent represents $dy/dx$. It demonstrates how each critical point on an implicit relation is detected by evaluating the slope of its tangent line. Source.

Interpreting dy/dx for Implicit Relations

To determine critical points, we first compute $dy/dx$ by differentiating the implicit equation with respect to x, treating y as a differentiable function. This process uses familiar rules such as the product rule and chain rule, but applied within the more general setting of an equation involving both variables. The resulting derivative often appears as a rational expression involving x, y, and sometimes multiple combined terms.

After determining this expression, we analyze where the derivative equals zero or fails to exist. These locations correspond to potential horizontal or vertical tangent lines, respectively. Because tangent behavior reflects local structure, such points mark where the curve changes direction, levels out, or becomes momentarily vertical in its orientation.

A key distinction arises when interpreting these cases. A derivative equal to zero indicates that the curve momentarily has no rise relative to run, forming a horizontal tangent. A derivative failing to exist suggests the slope becomes infinite or undefined, which corresponds to a vertical tangent. Both provide valuable insight into how the curve behaves in a neighborhood of the point.

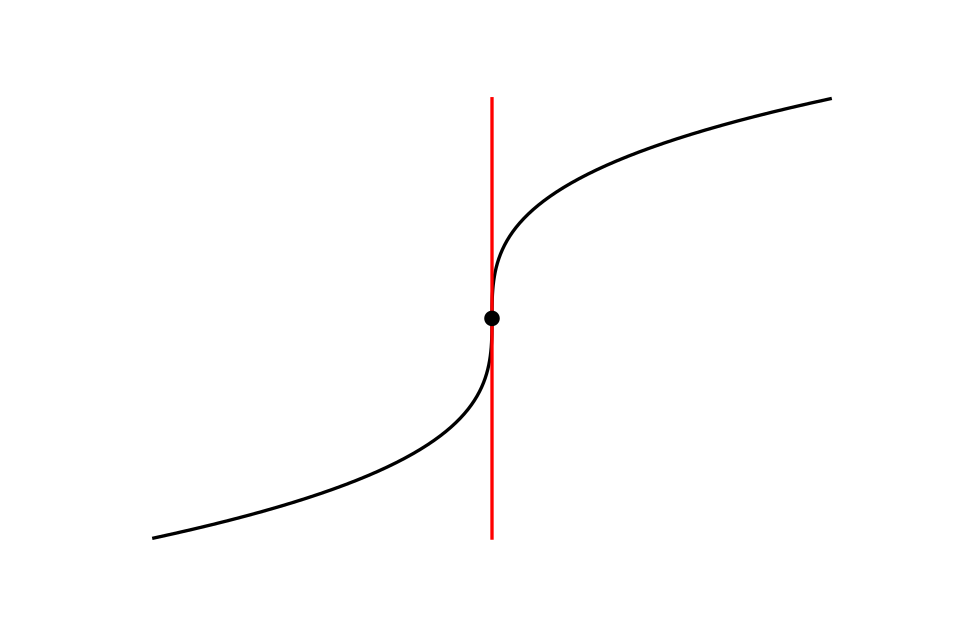
This image shows a curve with a clearly marked vertical tangent at the origin, where the derivative becomes undefined. It visually demonstrates how a vertical tangent corresponds to a point where $dy/dx$ does not exist, a key condition for critical points on implicit relations. Source.

Conditions Required to Identify a Critical Point

A point where $dy/dx = 0$ or $dy/dx$ is undefined does not automatically qualify as a critical point. The point must also satisfy the original implicit equation. This requirement preserves the logical connection between the derivative and the curve itself: slope values only make sense along points that belong to the relation. Therefore, verifying that each candidate point lies on the curve is essential.

To ensure accuracy when identifying critical points on implicit curves, students should follow a clear, logical process:

• Differentiate the relation implicitly, obtaining an expression for $dy/dx$ that reflects how both variables contribute to the slope.

• Determine where the derivative equals zero, indicating potential horizontal tangents.

• Find where the derivative is undefined, revealing points with potential vertical tangents.

• Check whether each candidate satisfies the original implicit equation, guaranteeing the point lies on the curve.

• Confirm that the x-value and y-value are within the domain of the relation, ensuring the point is meaningful within the context of the curve.

These steps help differentiate between algebraic possibilities and true geometric features of the implicit curve.

Geometric Meaning of Critical Points on Implicit Relations

When $dy/dx = 0$, the slope of the tangent line is horizontal. Geometrically, this corresponds to locations where the curve peaks, bottoms out, or otherwise levels before changing direction. Although identifying the precise nature of this behavior requires additional analysis, locating the point itself relies on the derivative structure.

When $dy/dx$ does not exist, the slope is vertical. Geometrically, the curve rises or falls without any horizontal motion, such as in a sideways cusp or a vertical tangent segment. These situations arise naturally in implicit relations, especially when the equation cannot be expressed cleanly as y as a function of x.

In both cases, the point’s validity as a critical point hinges on whether it belongs to the curve defined by the relation. The derivative alone cannot determine membership; only substitution into the original equation confirms the point’s presence on the curve.

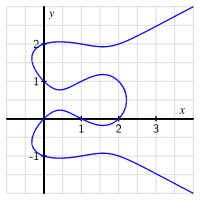
This diagram presents the implicit curve $x^3 + y^2 - 2xy = 2$ with a tangent line at the point $(-1,1)$, demonstrating how implicit differentiation identifies tangent behavior. It reinforces that critical points must satisfy both the derivative condition and the original implicit equation. Source.

Why Critical Points Matter for Implicit Curves

Critical points help illuminate a curve’s structure by identifying where important geometric behaviors occur. On implicit curves, these points often reveal turning behavior, cusp-like features, or changes in orientation. Understanding how derivatives behave in this context deepens students’ comprehension of calculus as a tool for analyzing curves beyond explicit function forms.